Learning Haskell

Phew! I’ve finally scratched the itch about what working in a Functional Programming language feels like. In the past when I want to expand my repertoire I’ve just picked an interesting language and built a toy, or done the Advent of Code. But for FP I knew that the "how do I do what I do in <familiar language> in <unfamiliar language>" would not do. I wanted to know "how do I use the principles of <unfamiliar language> to achieve what I could probably do in <familiar language>, but without stunting it with prior knowledge?".

Introduction

I picked Haskell because my shallow sense of it was that it is the granddaddy of FP but has nonetheless been kept current. It seemed strong on the ideals of FP, without the extreme sadism of APL. And I don’t know any popular disparaging memes about it like I do about the LISP family.

On day one I thought I’d be learning “Hello, world!” and then getting stuck into Monads and Functors. Turns out “Hello, world!” was one of the last lessons (and one of the most enlightening ones!) and Monads and Functors sort of came near the end and without much fanfare.

My pedagogical method was to work through Learn You A Haskell, transitioning to practice at Exercism, supplemented with long, windy, self-directed research.

In the end I punched out 50 exercises at Exercism. There's 96 in total but damn, what a workload. 50 is a fine goal before I wake up and I'm in my 90's. Every exercise I learnt something new, always thinking "finally, I'm competent, the next one will be a cinch" but then starting again at the bottom of another learning curve. After 50 I figure that Haskell is big enough that competence is a lofty goal, and familiarity is plenty worthy enough. But I'm an addict, so I did one more...

Pièce de Résistance

Alphametics are puzzles where words take the place of numbers in an equation, and your job is to figure out what number each letter represents. I fell in love with these from Adam Spencer's "Big Book of Numbers" recently, so couldn't resist the opportunity to solve them the computer science way. Haskell seems like a fun method!

And voila!

What a trip. This is super dense code. Like many of the Exercisms, this was a cycle of first figuring out a suitable algorithm, then figuring out a suitable implementation, and then cycling back to thinking about the algorithm such that a suitable implementation can be found. I take great pride in writing readable code, but finding that very difficult in Haskell. Reading other people's solutions (one of the many great features of Exercism) doesn't help much - for something of this complexity they are all very hard to read. I think that's the double-edged sword of highly terse languages - many ideal solutions look magnificent, but many practical solutions are impenetrable. I've found that establishing a style is a great way to foster readability, but in Haskell I've found it hard not to walk the path of arcane and inconsistent.

Nonetheless, this has been fantastic brain food. Undoubtedly it has met the goal of not just adding a tool to the toolbox, but casting the existing tools in a new light such that they all become more powerful.

GHCi, version 8.10.7: https://www.haskell.org/ghc/  :? for help
[1 of 2] Compiling Alphametics      (src/Alphametics.hs, interpreted )
[2 of 2] Compiling Paths_alphametics (Paths_alphametics.hs, interpreted )
Ok, two modules loaded.

*Paths_alphametics Alphametics> solve "SEND + MORE == MONEY"
Just [('D',7),('E',5),('Y',2),('N',6),('R',8),('O',0),('S',9),('M',1)]

Guided Walkthrough

If I found reading other people's solutions not always as illuminating as I would hope, I feel I may be of service by providing notes on interpreting mine, a few lines at a time. Open up the source code so you can follow along. Let's begin.

module Alphametics (solve) where

The boilerplate provided by Exercism expects your solution to be in a module called Alphametics and that you will expose a function called solve. The boilerplate wraps this in a test framework that checks your code with a set of validation inputs.

import Data.Char (isSpace)
import Data.List (nub, intersect, transpose, elemIndex)
import Data.Maybe (fromJust)

I used 3 libraries from the Data module, electing to specify the symbols I wanted explicitly so I knew exactly what was being imported and I don't pollute my namespace with everything in the library. All three libraries are in the base package which is distributed with Haskell, so I didn't need to install any additional dependencies. I've found that there are not many programs I can write without importing something from these three, given how fundamental the types Char, List and Maybe are. I wonder if I'm stuck reaching for these hammers even when my problem is not a nail?

solve :: String -> Maybe [(Char, Int)]

Again, this is provided in the boilerplate - we are expected to write a function called solve that accepts a String as an argument and returns a list of (Char, Int) pairs, maybe. In other words, if the String cannot be solve 'd, it should indicate that by returning Nothing instead of Just [(Char, Int)] .

solve input = if length solutions == 1 then Just $ zip charMap (head solutions) else Nothing

One of the biggest paradigm shifts in FP is to not think of a solution as a series of steps executed in order, but as a series of functions that can be combined to define the solution. In other words, instead of starting by creating all your variables and incrementally modifying them with flow control structures to eventually produce the output, you start with a definition of your output and provide all the sub-definitions necessary for that definition to be complete.

You can see how I grappled with understanding what it meant to think of the output first rather than the "preparation" first here. In one of the kindest responses I've had to a noob question on SO, I was encouraged to think that my feeble answer to my own question was on the right track. Thus, I've come to use the pattern in the solve input line a lot. That is, I tend to only put the last bit of window dressing in the first line. All the hard work happens later in the where expressions. Since solve returns a Maybe, I simply put the if statement in which ultimately produces the Nothing or Just according to the appropriate criteria.

This is a headspin for us lowly imperative souls, because at this point we haven't even produced anything that can be wrapped in a Just, let alone determined what the criteria would be for producing Nothing. But I've seen this pattern enough, and successfully used it enough now, that I'm confident it is often a sufficient and useful, if not necessary, pattern.

So in the end the solve input line foreshadows that solutions will contain our results, so all we need to check is if they are valid, then zip them up with charMap and return the result wrapped up in a Just, else return Nothing. Also, importantly, I have named the argument to solve (specifically, input) even though it is not used in that line. That's because I need to use it elsewhere and so am relying on closures in the where expressions to capture it without having to explicitly pass it down the line. This is a little reminiscent of global variables, which makes me a little uneasy. In imperative languages global variables are not to be avoided, necessarily, but certainly used with caution. I hope this usage in Haskell is an example of such judicious choice!

where
    toRowsOfChars       = wordsBy "+="                                
    toNonZeros          = map toNonZerosMap . nub . map head          
    toNonZerosMap x     = fromJust $ elemIndex x charMap              
    toColsOfChars       = transpose . map reverse                     
    toCharMap           = nub . concat                                

Now we start to work on the input. Most of these function are written point-free, in that they don't specify their argument. That's lovely, but it does mean you can't tell right away what the input is expected to be. That's the whole point of point-free, to promote generic usage, although it's a little moot in this case because these functions are very local and have specific purposes. I feel like if I were to make them usable generally, I'd have to come up with very wordy names to explain exactly what they do!

The to prefixes are a new style I came up with. I'm trying to write programs that consist just of long compositions of bite-size functions, but I tie myself in knots not being able to step out of the composition and take a rest with a variable, damn it. Even without using side-effects, I still want to keep variables around so I can use them "later". So I end up creating variables that are basically just the result of one of my functions. Even though I'm a big fan of naming functions with verbs and variables as nouns, I found that since functions are first-class citizens and therefore not otherwise distinguishable from variables, this still wasn't unambiguous enough.

So all my little functions in the composition chain are prefixed with to. That way I can still write them point-free, but retain the ability to name the outputs for self-documentation purposes.

toRowsOfChars converts the input (which is one big string like "SEND + MORE == MONEY") into a list containing each row, like ["SEND", "MORE", "MONEY"]. As is often the case in Haskell, this function started out more complicated, but ended up just calling a little helper function called wordsby. wordsby extends the words function found in the Prelude, by separating on the list of characters provided, as well as the space character that words acts on. Again, I'm sure there's a library for this, but I found it easier to just include an implementation than find a suitable library and install it!

The output of toRowsOfChars is expected as the input to toNonZeros and toColsOfChars. As foreshadowed, I keep this subtlety explicit by creating variables for each of the to functions.

toNonZeros creates the list of characters that cannot be zero. In Alphametics, letters that appear at the start of a word cannot be zero, which often turns out to be an essential restriction on the solution space. Reading the function definition from right to left (as we often do in Haskell), it pulls out the head (first char) of every word, removes duplicates (nub) then maps those chars to their index in the charMap using the toNonZerosMap helper.

toColsOfChars transposes the rows of chars into columns, right to left, which is exactly the way you're typically taught to do these sorts of sums in primary school - sum each column from right to left, carrying over any "tens" digit into the next column. Delightfully, I discovered this handles uneven length words perfectly, effectively right-justifying each word and producing shorter sub lists for the incomplete columns. Whenever I find myself swimming in the same direction as a programming language like this, I get a little spark of confidence that I'm starting to think in the language, rather than against it.

toCharMap produces an indexable map of each unique character. A list works fine for this purpose. Importantly, the indices run in the order in which each letter will be met when processing the output of toColsOfChars. This is crucial for ensuring we keep the solution space only as big as we need it for each column, instead of trying to solve for all letters at once.

toEncPuzzle :: [Int] -> [Char] -> [Int]
    toEncPuzzle acc x   = map encodeChar $ oldChars ++ newChars
      where
        oldChars      = take (length acc) charMap
        newChars      = intersect (nub x) $ drop (length acc) charMap
        encodeChar c  = let (lx:ix) = reverse x in -- create (last x) and (init x)
                        length (filter (==c) ix) + if c == lx then -1 else 0

Finally, we do some real work! Again, I'm using these temporal terms like "first" and "finally", as if this were an imperative language. In this case those terms simple refer to the order in the code, when in fact the execution order is quite different and determined by necessity, not specification. This is the magic behind laziness - you can define functions and variables in whatever order suits you, but Haskell will only execute them as it needs the outputs. That means you can define unnecessarily complete data structures, even infinite lists, without having to come up with terminating logic, and Haskell will only actually construct those structures as required.

toEncPuzzle is complicated enough that I justified giving it an explicit type signature (toEncPuzzle:: [Int] -> [Char] -> [Int]) and its own set of where expressions. The function is the first (temporally) major step in finding the solution. First we encode the puzzle into a structure that we can then solve. For each column (right to left), we create the minimal list which contains all new letters, as well as any letters we've seen so far. That list is then converted using charMap into a list of coefficients that describe the (zero) polynomial in that column. For example, if our charMap was "ABCDE" and our column was "A+C+A=D", then we would produce the list [2,0,1,-1,0] because, ignoring carries, the column equation is 2A + 0B + 1C - 1D + 0E = 0.

oldChars is the section at the start of charMap with length equal to the minimal list we've compiled so far. newChars is the rest of charMap, filtered by the characters in the current column using intersect.

The whole toEncPuzzle function will be wrapped in a scanl so that each column is processed in turn. The acc and x arguments are the "accumulation" and "current" values provided by each iteration of scanl.

toCandidates :: [([Int], Int)] -> [Int] -> [([Int], Int)]
-- p : current puzzle column, prev : result from previous column
-- a : all, o : old, n : new, co : carry out, ci : carry in
toCandidates prev p  = [(a,co) | (o,ci)<-prev, n<-digitCombs numNew,
                                 let a = o++n, nub a == a,
                                 co<-[0..length rowsOfChars - 2], ci + dot a p == 10*co]
  where numNew = length p - (length . fst . head $ prev)

Now we're on to the real powerhouse of this solution. All the heavy lifting happens in these 4 lines. I feel dirty using single character variable names, but it's a common convention and given the density of these constructs I can see why it's done. I consoled myself with a couple of lines of comments as a preamble.

toCandidates processes the output of toEncPuzzle, using a list comprehension to generate every possible solution, filtered by the constraints we currently know. This is a lovely example of defining "unnecessarily complete data structures" that never actually get created. A method for defining every solution was a journey, because while list comprehensions are super powerful, they are designed to use fixed generators. But I wanted a variable number of generators - one to produce [0..9] for every free variable in the column. After a bit of a rabbit warren exploration, I ended up piecing together digitCombs, which uses a trippy recursive list comprehension to do just that. Honestly I find these things hard to evaluate on paper, but easy enough to verify in code.

So now n is every possible solution to the free variables in the current column and o is all the solutions from the previous column. We also grab the carry out of the previous column, which becomes the carry in for the current column. The last generator is all the possible carry out values for the current column, which could be from 0 to 2 less than the number of rows. That's because the worse case for n rows is 9+9+...+9=x where x doesn't contribute to carry out and n*9 will give a carry out of (n-1).

With the generators in place, we then decimate the combinations with the predicates. First we combine the old and new solutions and call it a. Then we restrict the results to those that do not repeat a number using nub a == a, and to those that satisfy the column equation using ci + dot a p == 10*co. This says that the carry in, plus the column polynomial, equals ten times the carry out. I couldn't find a dot product function in the Prelude to produce the polynomial from coefficients and variables, so I included one in the solution. Although it's a simple formula, I wouldn't have figured out the necessity for the extra . between sum and zipWith without extra research. Turns out you can't compose a two argument function (zipWith (*)) with a single argument function (sum) using .. If you do the maths with the . operator you find an additional one pops out. Alternatively I could have used fmap sum but I don't think that would have been any more obvious. Apparently the double . convention is widely used.

Note my natural inclination is to put all the generators first and the predicates (or more specifically, "guards", eg. nub a == a)  last, but hlint suggests otherwise and I dislike squiggly lines more than I have confidence in my style preference.

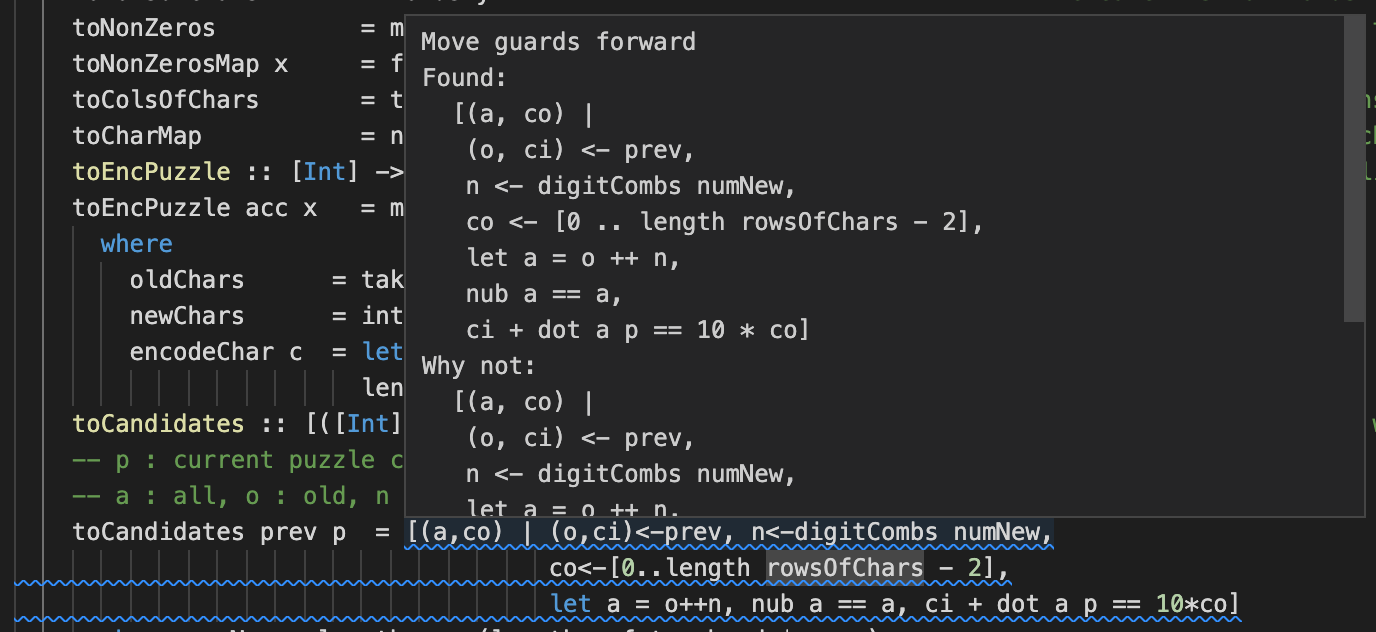
And that's about it for toCandidates. The results of the current column are returned so that when called from foldl they will be available to the next column as prev. By the time foldl has gone through each column we will have built up a list of all free variables, trimmed at each column by the constraints at that column.

toSolutionsPrelim   = map fst . filter (\x -> snd x == 0)
toSolsFold acc x    = filter (\sol -> (sol !! x)  /= 0) acc

All that's left to do is take the output of toCandidates and apply two more constraints. toSolutionsPrelim strips out all the solutions that were left with a carry out from the final column, cause maths don't work like that. It also applies a sneaky map fst because that's where the solution is. snd contains the carry out and we not longer care about it. I feel this contravenes the general design principle that Haskell encourages, but damn, this solution is complex enough already without trying to write each line as if it could be used on any input. Again I console myself by noting that all these functions are part of a where clause, so at least no one thinks they can be used outside of solve without some extra work.

toSolsFold applies one more constraint - when called using foldl on nonZeros, those solutions that picked 0 for one of the letters that cannot be zero, will be dropped. This is a slightly trippy little operation too - the input to foldl is nonZeros even though the output is the filtered version of solutionsPrelim. There's nothing stopping this from happening - whatever you accumulate in acc is what gets output from foldl, and in this case I seed it with all of solutionsPrelim instead of some empty set like is often done with foldl. But it did throw me for a while that this was the solution I was steered myself to.

-- Below are all the intermediate results for each of the `to` functions above.
rowsOfChars         = toRowsOfChars input
nonZeros            = toNonZeros rowsOfChars
colsOfChars         = toColsOfChars rowsOfChars
charMap             = toCharMap colsOfChars
encodedPuzzle       = tail $ scanl toEncPuzzle [] colsOfChars
candidates          = foldl toCandidates [([],0)] encodedPuzzle
solutionsPrelim     = toSolutionsPrelim candidates
solutions           = foldl toSolsFold solutionsPrelim nonZeros

As foreshadowed, the remainder of the solve function is just applications of all the to functions that have been defined above. As suggested, I found this useful because I get to give the output of each function a name to help with self-documentation, and I get to branch off in several directions instead of being caught in the linear process groove of a composition train.

And there you have it, 50 lines of Haskell after 50 practice exercises, with about 50 brain explosions baked into each line.

Pre Musing

I love the thrill of being a good amateur. I wanted to try to capture some of that fumbling-in-the-dark wonder before the curse of knowledge takes hold. So I thought it might be interesting to write down my preconceptions, before I lose touch with the innocence of naivety.

To wit, my list of naive assumptions, together with some selected learnings in italic.

• Haskell is the cream of Functional Programming (FP).
  • Arguably, at least in the pragmatic sense. It's been around long enough to be considered mature, but it seems it also managed to break free of its origins around the great Haskell 98 bifurcation. Modern Haskell has kept with the times, staying true to key ideals while remaining relevant during the recent FP renaissance.
• FP is about programming in a world that is stateless, side-effect free, idempotent and composable, because those restrictions are powerful. Those powers are:
  1. elimination of bugs that occur only under certain pre-conditions, and in particular heisenbugs. Essentially it's the logical enforcement that all bugs are system faults (as opposed to random faults) because software is deterministic.
  2. reasonability, which provides both the programmer (human) and programmer (computer) optimal conditions for both proving and refactoring. In other words, the restrictions of FP produce something that can be manipulated mathematically with impunity such that any logical derivation is a true and complete representation of the original. No "context" or "but in the real world" applies.
  • Pretty close, actually.
• On the other hand, people seem to associate FP with monads, applicatives and functors. I don't know what the overlap between stateless et al. and monoid combinators et al is.
  • Turns out those terms are largely design details.
• Being stateless, FP is highly impractical. That doesn't lessen it's worth as an academic tool, but given that something so fundamental as I/O requires side-effects, FP seems live in a domain that can't impact the real world.
  • Would be true in pure FP. In Haskell side-effects are a core feature, but are water-tightly isolated.
• stack and cabal are two alternatives to dependency management, akin to cargo or shards. But like Homebrew and MacPorts, or apt and rpm, or pip and conda, there are many modern pitfalls around local/global/project environments, versions and conflicting managers.
  • stack is not just dependency management, but project management (creation, build, test, etc.) akin to rails. The co-existance is reminisicant of pip and conda though.
• Imperative style and side-effects are bad, or at least undermine the potential benefits of FP, so using those crutches should be avoided. Which makes do and Lens and other intricate methods for re-introducing those basic principles weird.
  • No. do and Lens are deliberately constructed tools for doing essential side-effect laden I/O and mutable structures, respectively, without tainting the FP program at large.
• if is to be avoided because it's getting imperative. Definitely avoid else if.
  • Yeah, pretty much, although a simple if/then/else is perfectly reasonable at times.
• Closures are bad because the function is no longer pure.
  • *No! Haskell is very deliberate about this. Closures (and free variables in Haskell) are fine because they are immutable. Only mutable state invalidates pureness. Great discussion here.
• In FP you can't do something to something, and also something else to that something. If you can't define your problem as a pipeline, then you're going to struggle.
  • Except that's what the Φ / S' / Pheonix / Starling' Combinator does, which is all the rage...
  • Not at all. Lots of ways to do just that without diluting pureness.
• Pattern matching can only be done in a top-level function.
  • Nope
• A Functor is like a function in that it applies to an input.
  • Nope, it's more like a container with special properties.
• A Monad is a fundamental construct.
  • Nope, a Functor is far more fundamental. A Monad is a generalised Applicative, which is a generalised Monad.
• FP has a powerful explict assumption that everything will go as you expect. The classic if fail idiom doesn't exist and it's painfully hard to insert one. In theory you can control your inputs and never fail. In practice it's probably going to fail.
  • More research necessary. The Maybe and Either constructs are for failure handling, while exceptions are powerful but really only for I/O. Need to see it working in a larger example to understand how practical it is.
• Learn You A Haskell's focus on functions first is a reflection of the fact that Haskell is not an application programming language, but an interesting tool for solving problems in isolation from the user.
  • Not entirely. You need to think functions first, so it's a good place to start, but all the trappings of an application language are there too.
• Learn You A Haskell introduces I/O very late because it's a minor, ugly cousin feature of the language.

The last one in particular is interesting in its naivety. I suspended judgement on the merit of lazy, pure, infinite-lists-are-okay, stateless, FP for a long time, and finally started to conclude that Haskell provides a very interesting, but in rarely superior method of programming. Then the I/O chapter points out that if you apply interact to your point-free FP function, it runs forever evaluating only what it needs to when it needs to! That's the kind of unexpected consequence that makes academic explorations rather delightful.

Post Musing

I still find FP frustratingly otherworldly, despite feeling okay with the general techniques. Straining through this 2 hour presentation by the author of a Haskell package for Lenses left me feeling that these people know some things, but you gotta be in the know, you know? https://www.youtube.com/watch?v=cefnmjtAolY

So many times I’d emerge from a brain beating on a new concept and think, wait, is that all it was all along?

Wait, are Monads just the pairing of a data wrapper and a method for applying functions to the data without getting it out of the wrapper, so they can be used FP style?

Wait, are Lenses just getters and setters that can be used FP style?

I guess that’s the appeal of Haskell - it’s a research tool that lets you really understand what it takes to make something that “can be used FP style” and to push the boundaries of what “FP style” is. For a practitioner, that’s a lot of detail. But for a comp sci researcher, or a compiler designer, or someone else interested in poking the beast, Haskell is where it’s at..

I got the sense actually, that Haskell is a tool for making generalisations. Sure, an array is a handy construct for certain purposes that can do certain things. But what if there was no array, man. What if we didn’t get so specific about it, and just came up with operations that work, in general. Then every problem you could ever come up with would start to look like a problem that had already been solved (or has not, in which case you can probably just give up early). It’s a very strong technique in maths. I often feel Haskell is a method for bringing the same to programming, but given the interests of those wishing for such a world, probably favours the pursuit of abstraction rather than the stated goal of actually putting abstractions to work.

Epilogue

While writing this post, I left a compiled version of my solution running on a 10 letter, 200 line input. It finished just as I finished the first draft.

$ time solve "THIS + A + FIRE + THEREFORE + FOR + ALL + HISTORIES + I + TELL + A + TALE + THAT + FALSIFIES + ITS + TITLE + TIS + A + LIE + THE + TALE + OF + THE + LAST + FIRE + HORSES + LATE + AFTER + THE + FIRST + FATHERS + FORESEE + THE + HORRORS + THE + LAST + FREE + TROLL + TERRIFIES + THE + HORSES + OF + FIRE + THE + TROLL + RESTS + AT + THE + HOLE + OF + LOSSES + IT + IS + THERE + THAT + SHE + STORES + ROLES + OF + LEATHERS + AFTER + SHE + SATISFIES + HER + HATE + OFF + THOSE + FEARS + A + TASTE + RISES + AS + SHE + HEARS + THE + LEAST + FAR + HORSE + THOSE + FAST + HORSES + THAT + FIRST + HEAR + THE + TROLL + FLEE + OFF + TO + THE + FOREST + THE + HORSES + THAT + ALERTS + RAISE + THE + STARES + OF + THE + OTHERS + AS + THE + TROLL + ASSAILS + AT + THE + TOTAL + SHIFT + HER + TEETH + TEAR + HOOF + OFF + TORSO + AS + THE + LAST + HORSE + FORFEITS + ITS + LIFE + THE + FIRST + FATHERS + HEAR + OF + THE + HORRORS + THEIR + FEARS + THAT + THE + FIRES + FOR + THEIR + FEASTS + ARREST + AS + THE + FIRST + FATHERS + RESETTLE + THE + LAST + OF + THE + FIRE + HORSES + THE + LAST + TROLL + HARASSES + THE + FOREST + HEART + FREE + AT + LAST + OF + THE + LAST + TROLL + ALL + OFFER + THEIR + FIRE + HEAT + TO + THE + ASSISTERS + FAR + OFF + THE + TROLL + FASTS + ITS + LIFE + SHORTER + AS + STARS + RISE + THE + HORSES + REST + SAFE + AFTER + ALL + SHARE + HOT + FISH + AS + THEIR + AFFILIATES + TAILOR + A + ROOFS + FOR + THEIR + SAFE == FORTRESSES"

Just [('S',4),('A',1),('E',0),('R',3),('L',2),('I',7),('T',9),('F',5),('O',6),('H',8)]
real	64m26.172s
user	62m55.259s
sys	0m24.466s

Impressive. To be fair though, I haven’t checked the answer ;-)

For context, an earlier iteration of my solution could manage "I + BB == ILL" but never saw the end of "SEND + MORE == MONEY". The current version does it in the blink of an eye. I have learnt to expect that these algorithmic solutions either finish right away, or never, so I’m rather impressed the 64 minutes effort was bounded.